Eliminators are undoubtedly the most difficult aspect of type theory. In this article we will try to make more clear how they work, but most importantly why we need them. This articles will present some analogies between eliminators and constructs of programming languages (such Python, Rust, Scala, …) which can help who knows some basic of computer programming understanding eliminators. Agda will be used to implement all eliminators, since it is a language (and proof assistant) built on top of Martin-Löf’s type theory.

$$\newcommand\norm[1]{\left\lVert#1\right\rVert}$$ Given v⃗, u⃗ ∈ ℝn with $\vec{v}=\norm{\vec{v}}\hat{v}$ and $\vec{u}=\norm{\vec{u}}\hat{u}$, we can write $$\ln\vec{v}=\ln\left(\norm{\vec{v}}\hat{v}\right)=\ln\norm{v}+\ln\hat{v}$$ Now let’s take the plane spanned by the two vectors: S = ⟨v⃗, u⃗⟩. In this plane we can fix a Gauß plane in order to calculate ln v̂: ln v̂ = (∠v̂+γ)i where γ ∈ ℝ is an arbitrary constant, derived from the fact we cannot know the real phase of v̂ in the Gauß plane, since it depends on how we fixed the axis.

From the point of view of biology and botanic a tomato is a fruit, but from the point of view of food it is commonly considered a vegetable. So how to distinguish between culinary fruit and vegetables? We will train a simple linear binary classification with the aim to distinguish culinary fruit from vegetables taking in account the fact it is botanically a fruit, the fact that it grows on tree or not, the fact that it grows underground or not, and nutritional informations.

We will now explore some methods to approximate the fraction $$\frac{A}{1+B}\quad\quad\text{with } B\in(-1,1)$$ Let’s start with an iterative algorithm which starts from A − AB and at each iteration obtains a closer value to the desired result: Iterative algorithm to approximate $\frac{A}{1+B}$ Input: $A; B\in(-1,1)$ Output: $x\approx\frac{A}{1+B}$ $x = A$; until $x$ has a stable enough value do | $x \leftarrow A - Bx$; done return $x$; We can describe the algorithm also in a recursive way: \begin{aligned} f(x) &= A - Bx\\ \frac{A}{1+B} &\approx f^n(A) = \underbrace{f\left(f\left(\dots f(A))\right)\right)}_n\quad n\text{ big enough} \end{aligned}

Will time machines be build? The probability that in future a time machine that can travel to the past would be build is very low.

A tour of the meaning of “sacredness”, from the origin of the word, to our days.

$$\newcommand\norm[1]{\left\lVert#1\right\rVert}$$ Scalarization # Definition 1. Given $\underline{f}: \mathbb{R}\supseteq D \rightarrow \mathbb{R}^n$ $$שׂ\underline{f}: D \rightarrow \mathbb{R}$$ $$שׂ\underline{f}(x) := \int_0^x\norm{\frac{\mathrm{d}\underline{f}(u)}{\mathrm{d}u}}\mathrm{d}u+\norm{\underline{f}(0)}$$ Where ∫0xg(u) du is the primitive $\overline G(x)$ of g(x), with $\overline G(0) = 0$. Theorem 1 (Scalarization of constant). Given $\underline{a}\in \mathbb{R}^n$ $$שׂ\underline{a}= \norm{\underline{a}}$$ Proof. $$שׂ\underline{a}= \int_0^x\norm{\frac{\mathrm{d}\underline{a}}{\mathrm{d}u}}\mathrm{d}u+\norm{\underline{a}} = \int_0^x0\mathrm{d}u+\norm{\underline{a}} = \norm{\underline{a}}$$ ◻ Remark 1. We will interpret $$שׂ\underline{f}(\overline x) = [שׂ(\underline{f})](\overline x)$$ because for Theorem1 $$שׂ(\underline{f}(\overline x)) = \norm{\underline{f}(\overline x)}$$ isn’t very usefull.

$$\newcommand\norm[1]{\left\lVert#1\right\rVert}$$ Definition 1. Scalar area product in ℝ3. Given $\underline{a}, \underline{b}\in \mathbb{R}^3$ $$\underline{a}\dot\wedge\underline{b}:= \norm{\underline{a}\wedge \underline{b}}$$ Where $\underline{a}\wedge \underline{b}$ is the vector product between the two vectors. Theorem 1 $$\underline{a}\dot\wedge\underline{b}= \sqrt{\norm{\underline{a}}^2 \norm{\underline{b}}^2 - (\underline{a}\cdot\underline{b})^2}$$ Where $\underline{a}\cdot \underline{b}$ is the usual scalar product between the two vectors. Proof. $$\underline{a}\cdot\underline{b}= \norm{\underline{a}}\norm{\underline{b}}\cos\theta \implies \cos^2\theta = \left(\frac{\underline{a}\cdot\underline{b}}{\norm{\underline{a}}\norm{\underline{b}}}\right)^2$$ $$\sin^2\theta = 1 - \cos^2\theta = 1 - \left(\frac{\underline{a}\cdot\underline{b}}{\norm{\underline{a}}\norm{\underline{b}}}\right)^2$$ $$\underline{a}\dot\wedge\underline{b}= \norm{\underline{a}\wedge \underline{b}} = \norm{\underline{a}}\norm{\underline{b}}\sin\theta =$$ $$= \norm{\underline{a}}\norm{\underline{b}}\sqrt{1-\left(\frac{\underline{a}\cdot\underline{b}}{\norm{\underline{a}}\norm{\underline{b}}}\right)^2} = \sqrt{\norm{\underline{a}}^2 \norm{\underline{b}}^2 - (\underline{a}\cdot\underline{b})^2}$$ ◻

Nel 1948 George Orwell scriveva “1984”: un romanzo distopico nel quale si racconta di una società totalmente sorveglia dalle telecamere del Grande Fratello; ebbene in questi giorni sui social si sta facendo strada la notizia ( anche se non è una novità) che in Cina ci sono effettivamente delle telecamere che sorvegliano ogni singola persona assegnandole un punteggio (social credit) sulla base del quale gli vengono erogati o meno dei servizî (trasporti, istruzione,social credit, connessione a internet, offerte di lavoro, …).

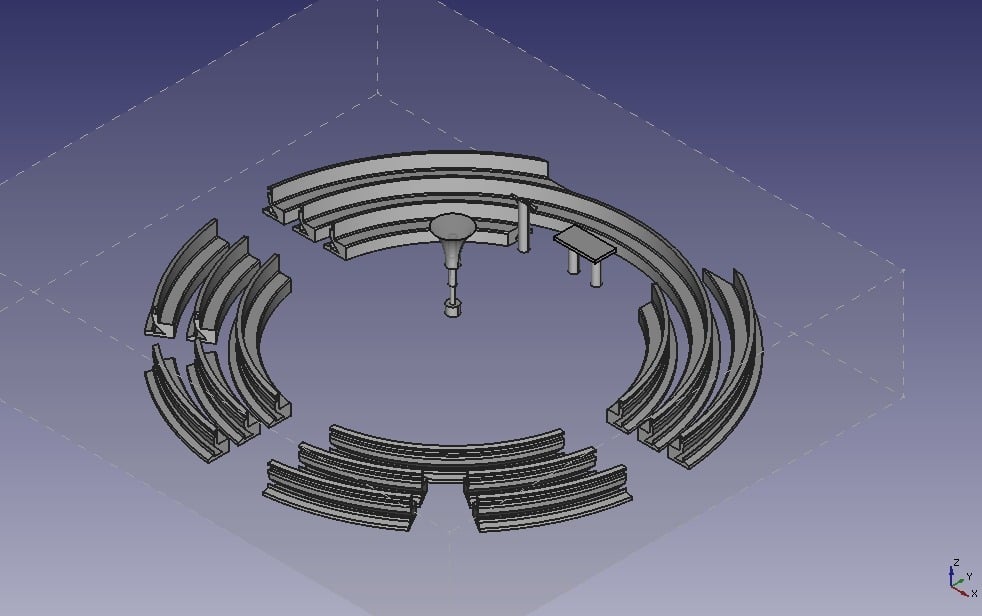
Link to project: https://www.thingiverse.com/thing:2791347 “Our Father who are in heaven” (Mt 6:9-13) We are all siblings each other: being all in a circle makes us feel united. The tabernacle, with the body of Christ, is in the center of the circle; so all are turned towards Jesus, not only the people. The tabernacle is the top of a tree with the roots in Heaven. It contains Jesus, who brings Heaven on earth.